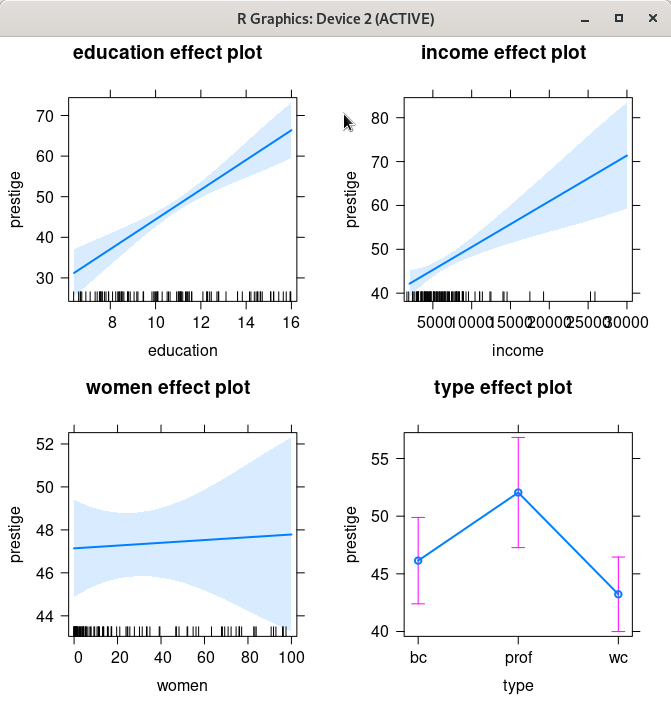
MASS 패키지에는 birthwt라는 데이터셋이 포함되어 있다. birthwt 데이터셋을 활용하여 bwt라는 2차 데이터셋이 만들어진다.
bwt <- with(birthwt, {
race <- factor(race, labels = c("white", "black", "other"))
ptd <- factor(ptl > 0)
ftv <- factor(ftv)
levels(ftv)[-(1:2)] <- "2+"
data.frame(low = factor(low), age, lwt, race, smoke = (smoke > 0),
ptd, ht = (ht > 0), ui = (ui > 0), ftv)
})
bwt <- with(birthwt, {
race <- factor(race, labels = c("white", "black", "other"))
ptd <- factor(ptl > 0)
ftv <- factor(ftv)
levels(ftv)[-(1:2)] <- "2+"
data.frame(low = factor(low), age, lwt, race, smoke = (smoke > 0),
ptd, ht = (ht > 0), ui = (ui > 0), ftv)
})
bwt 데이터셋은 분석 모형을 만드는데 간혹 예제로 사용되는데, birthwt에서 bwt가 만들어지는 과정이 R Commander 기본 사용자에게는 다소 어렵게 느껴질수 있겠다는 판단이다. 데이터셋 자체에 대한 이해의 어려움 때문에 분석 모형의 구성과 해석으로 나아가지 못하는 경우가 있어, bwt 데이터셋 설명을 하고자 한다.
bwt 데이터셋은 저체중아 출생의 원인을 찾고자 하는 문제의식을 담고 있다. low 변수는 출생당시 몸무게가 2.5kg 미만 여부를 담고 있으며, 반응변수가 된다. 나머지 변수들은 저체중아 출산에 영향을 끼치는가 여부인 설명변수들의 후보군이 되겠다.
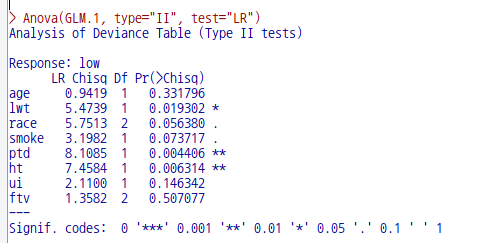
options(contrasts = c("contr.treatment", "contr.poly"))
GLM.1 <- glm(low ~ ., binomial, bwt)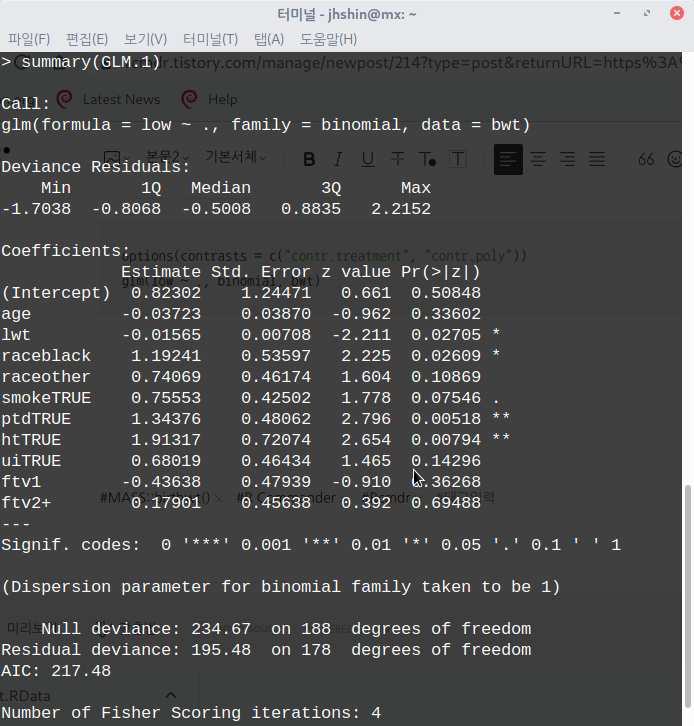
'Dataset_info > birthwt' 카테고리의 다른 글
| birthwt 데이터셋 (0) | 2022.03.09 |
|---|