4. RESET test for nonlinearity...

모델 > 수치적 진단 > 비선형성에 대한 RESET 검정...

Models > Numerical diagnostics > RESET test for nonlinearity...

Linux 사례 (MX 21)

데이터셋 하나를 만들어보자. x, y1, y2라는 변수를 가진 rawData라는 데이터셋이다.

x <- c(1:30)
y1 <- 1 + x + x^2 + rnorm(30)
y2 <- 1 + x + rnorm(30)
rawData <- as.data.frame(cbind(x, y1, y2))

rawData 데이터셋을 활성화시키자. <활성 데이터셋 없음>을 누르면 활성데이터셋 후보에 rawData가 있을 것이다. 두개의 단순 회귀 모형을 만든다.

RegModel.1 <- lm(y1 ~ x, data=rawData)
summary(RegModel.1)
RegModel.2 <- lm(y2 ~ x, data=rawData)
summary(RegModel.2)

'모델 > 수치적 진단 > 비선형성에 대한 RESET 검정...'을 RegModel.1, RegModel.2에 각각 시행한다. RESET 검정의 하위 메뉴 창이 등장한다. 기본 설정을 그대로 사용하고, 예(OK) 버튼을 누른다.

Linux 사례 (MX 21)

Linux 사례 (MX 21)

RESET은 Regression Equation Specification Error Test의 약자이다.

RegModel.1과 RegModel.2의 분포적 특징을 산점도를 활용하여 먼저 시각적으로 살펴보자.

Linux 사례 (MX 21)

Linux 사례 (MX 21)

첫째 그래프인 plot(y1, x)의  점들의 분포는 선형이라는 보다는 이차방정식적(quadratic)으로 보인다. 그렇다면, lm(y1 ~ x)라는 선형 회귀 모형을 lm(y1 ~ x + I(x^2))라는 이차방정식적 회귀 모형으로 변화시켜 만들어볼 수 있지 않을까?

RegModel.1_1 <- lm(y1 ~ x + I(x^2), data=rawData)
summary(RegModel.1_1)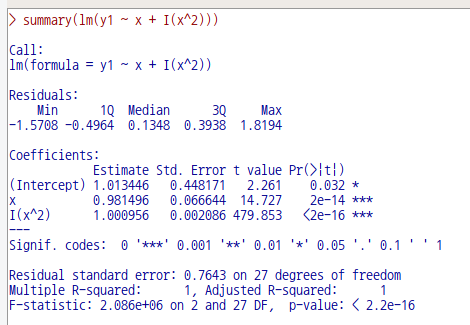

Linux 사례 (MX 21)

RegModel.1_1이 RegModel.1보다 모형의 설명력이 높다고 할 수 있다.